Математические основы финансового менеджмента
Рисунок – Определение будущей наращенной стоимости разового платежа
Для решения этой задачи используются специальные формулы наращения (см. таблицу 1).
Таблица 1 – Основные формулы наращения с применением различных типов ставок
|
Область применения |
Ссудный процент |
Учетная ставка | |
|
Простые проценты | |||
|
Определение будущей стоимости при целом числе лет «n» |
|
| |
|
Определение будущей стоимости при продолжительности периода в днях |
|
| |
|
Сложные проценты | |||
|
Определение будущей стоимости при целом числе лет, «n» |
|
| |
|
Определение будущей стоимости, когда начисление процентов производится «m» - раз в году |
|
| |
где
n – период начисления, количество лет;
t – продолжительность периода начисления в днях;
T – продолжительность года в днях;
m - число начисления процентов в году;
FM1 (r,n) = (1+r)n – фактор будущей стоимости текущего капитала, множитель наращения сложных процентов или мультиплицирующий множитель. Табличные значения множителя наращения FM1 (r,n) приведены в Таблице 1 Приложения.
В зависимости от способа определения продолжительности финансовой операции рассчитывается либо точный, либо обыкновенный (коммерческий) процент.
Дата выдачи и дата погашения ссуды считаются за один день. При этом возможны два варианта:
- используется точное число дней ссуды, определяемое по специальной таблице, где показаны порядковые номера каждого дня года; из номера, соответсвующего дню окончания займа, вычитают номер первого дня (см. формулы 1.2 и 1.2.1);
- берется приблизительное число дней ссуды, когда продолжительность полного месяца принимается равной 30 дням (см. формулы 1.2 и 1.2.1); этот метод используется, когда не требуется большая точность, например, при частичном погашении займа.
Точный процент получают, когда за временную базу принимают фактическое число дней в году (365 или 366) и точное число дней ссуды.
Пример.
Задача, по сути, являющаяся алгоритмом, позволяющим решать разнообразные инвестиционные проблемы, может быть сформулирована следующим образом:
Какая сумма будет накоплена вкладчиком через три года, если первоначальный взнос составляет 400 тыс. тг., проценты начисляются ежегодно по ставке 10%?

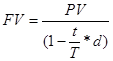 (1.2.1)
(1.2.1) 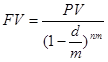 (1.4.1)
(1.4.1)